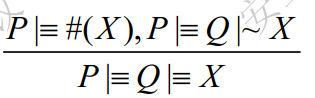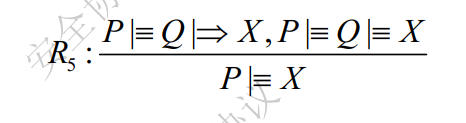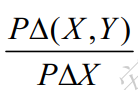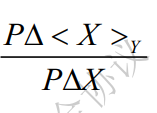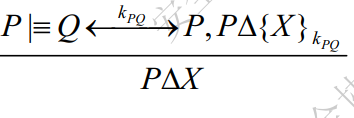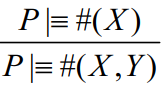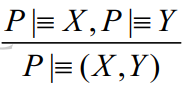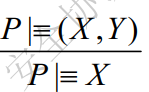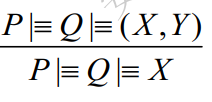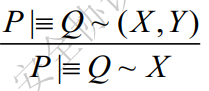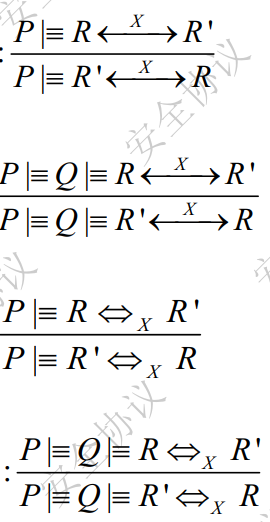安全协议分析,主要为BAN逻辑
安全协议安全性分析方法
主要方法
- 可证明安全性理论与方法
- 形式化分析理论与方法
- 混合理论与方法
- 零知识证明理论与方法
- 安全多方计算理论与方法
BAN逻辑
BAN逻辑是一种形式化分析方法。
安全协议形式化分析主要技术
- 逻辑方法:采用基于信仰和知识逻辑的形式分析方法,比如以BAN逻辑为代表的类BAN逻辑
- 通用形式化分析方法:采用一些通用的形式分析方法分析安全协议,例如应用Petri网等
- 模型检测方法:基于代数方法构造一个运行协议的有限状态系统模型,再利用状态检测工具来分析安全协议
- 定理证明方法:将密码协议的安全性做为定理来证明,这是一个新的研究热点
BAN逻辑系统假设
- 时间假设
- 协议分析中区分两个时间段,过去时间段和当前时间段。
- 当前时间段开始于协议运行的开始阶段,所有在此时间之前发送的消息都认为是在过去时间段发送的消息。
- 如果信仰在开始时成立,则在整个当前时间段都成立,而在过去时间段成立的信仰,在当前时间段不一定成立。
- 密钥假设
- 加密系统是完善的,只有知道密钥的主体才能解读密文消息,任何不知道密钥的主体都不能解读密文消息,也没有办法根据密文推导密钥
- 密文块不能被算改,也不能用几个小的密文块来拼凑成一个新的大的密文块,一个消息中的两个密文块被看作是分两次分别到达的
- 密文含有足够的冗余消息,解密者可以根据解密的结果来判断他是否已经正确解密
- 消息中有足够的冗余消息,使得主体可以判断该消息是否来源于自身
- BAN逻辑还假设协议的参与主体是诚实的
BAN逻辑的语法、语义
- BAN逻辑是一种多类型模态逻辑 (many-sorted model logic)
- BAN逻辑的语义中主要包含下面三种处理对象:
- 主体(principals)
- 密钥(keys)
- 公式(formula),也被称为语句或命题(statements)
- 符号规定
- A,B表示主体,S表示服务器
- $K_{ab}$、$K_{as}$和$K_{bs}$表示共享密钥,$K_a$、$K_b$,和$K_s$表示公开密钥,$K_a^{-1}$,$K_b^{-1}$表示相应的秘密密钥
- $N_a$、$N_b$等表示随机数
- P、Q、R等表示主体变量,K表示密钥变量,X、Y表示公式变量。
- 包含和取这一种命题连接词,用逗号表示
| 符号 | 语义 |
|---|---|
| $P$、$Q$ | 主体变量,泛指参与协议的各方 |
| $X$ | 公式变量,泛指协议中消息的含义 |
| $P | = X$ |
| $P\Delta X$ | $P$看见$X$ |
| $P | \sim X$ |
| $P | \Rightarrow X$ |
| $#(X)$ | $X$是新鲜的 |
| $P\overset{k}{\longleftrightarrow}Q$ | $P$和$Q$共享仍具有保密性的密钥$k$ |
| $\overset{k}{\longrightarrow}P$ | $P$具有公钥$k$(对应私钥为$k^{-1}$),私钥只有$P$及他信任的人持有 |
| $P\Leftrightarrow_X Q$ | $P$和$Q$共享秘密$X$ |
| $P\overset{k}{\longleftrightarrow}Q$ | 用$K$加密$X$后的消息 |
| $ |
$X$与秘密$Y$合成的消息 |
BAN逻辑的推理规则
消息含义规则
共享密钥情况
$$
\frac{P|\equiv Q\overset{k_{PQ}}{\longleftrightarrow}P,P\Delta {X}{k{PQ}}}{P|\equiv Q|\sim X}
$$公钥情况
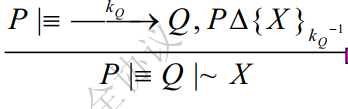
共享秘密情况
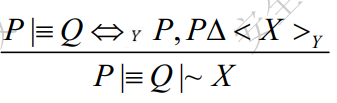
随机数验证规则(nonce-verification rule)
管辖规则
接收消息规则(seeing rules)
新鲜性规则
信仰规则(belief relus)
密钥与秘密共享规则(key and secret rules)